Der Brummi nachgerechnet: Flugleistungen

Leistungsdiagramm

Da in Excel alles tabellarisch gerechnet wird, fällt wiederum die grafische Darstellung der Leistungsdaten in Kurven leicht. Berechnet wurden, wie üblich, die Gegenüberstellung von Propellerschub und Widerstand sowie der Leistungen von Antrieb und Zelle. Letztere wird hier gezeigt.

Zunächst kann man dem Bild entnehmen, daß der gewählte Geschwindigkeitsbereich von 6 bis 12 m/s paßt. In diesem Bereich sind der Leistungsbedarf des Modells (gelb) sowie das Leistungsangebot des Antriebs bei Vollast (violett) und Teillast (dunkelblau) dargestellt. Teillast entspricht der im Horizontalflug ermittelten Leistung. Zusätzlich wird die für das Steigen verfügbare Leistung bei Vollast als Differenz (hellblau) gezeigt. Schließlich ist auch die mit einer Akkuladung maximal erreichbare Höhe (violett gestrichelt) eingetragen.

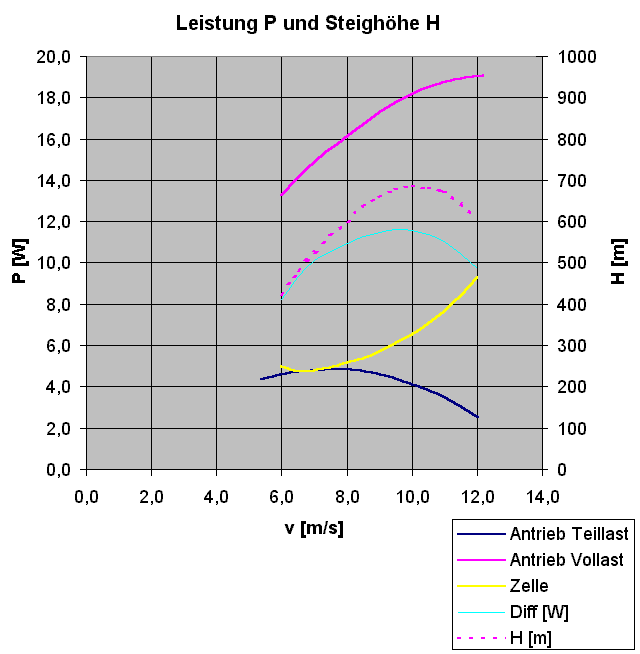
Es sollte auffallen, daß größte Steigleistung und größte Steighöhe bei verschiedenen Fluggeschwindigkeiten erzielt werden. Man kann aus den Leistungskurven nicht ohne weiteres auf das beste Steigen schließen, auch nicht auf das beste Sinken. Dafür braucht man die Polaren, die weiter unten gezeigt werden.

Festzuhalten ist auch noch , daß mit der für Teillast angenommenen Leistung das Modell gerade in der Luft gehalten werden kann. Es befindet sich dabei aber in einem labilen Gleichgewicht: Jede kleine Störung, welche die Geschwindigkeit verringert oder erhöht, vergrößert den Leistungsbedarf, während die Antriebsleistung abnimmt. Den Energieverlust muß man entweder mit Höhenverlust oder mehr Leistung ('Gas') bezahlen. Wegen des stabilen Fluges fliegt man deshalb praktisch mit höherer Leistung bei höherer Geschwindigkeit (z.B. 8 m/s). Hier wird nur das absolute Minimum der Schwebeleistung demonstriert.

Polaren

Die Polaren entstehen, wie die Leistungskurven, aus den aerodynamischen Daten des Modells. Im Prinzip werden ganz einfach die Werte der einzelnen Komponenten (Flügel, Rumpf, Leitwerk, Fahrwerk) ermittelt und addiert. Bei verschiedenen angenommenen Fluggeschwindigkeiten muß immer der Auftrieb des Flügels dem Gewicht des Modells entsprechen, was verschiedene Auftriebsbeiwerte bedeutet. Diesen wiederum entsprechen die Widerstandsbeiwerte, und so kann man den Widerstand des Flügels berechnen. Für die anderen Komponenten werden Widerstandsbeiwerte angenommen. Die Widerstände aller Komponenten werden aufsummiert und um einen geschätzten Interferenzwiderstand ergänzt. Jetzt lassen sich auch die Vertikalgeschwindigkeiten ermitteln.

Der Flügel spielt dabei natürlich die Hauptrolle. Er erzeugt im wesentlichen den Auftrieb, und er hat neben dem Profilwiderstand den sehr beachtenswerten induzierten Widerstand. Die Werte lassen sich mit brauchbarer Genauigkeit bestimmen, nur sollte man ab der zweiten numerischen Stelle keine Wunder an Genauigkeit erwarten. Das ist auch nicht nötig, denn es gibt ein wichtigeres Problem: Das Modell kann nur bei einer Fluggeschwindigkeit ausgetrimmt sein. Häufig stellt man es so ein, daß dann das Höhenleitwerk keinen Auf- oder Abtrieb liefert. Bei allen anderen Geschwindigkeiten tut es das aber, so daß der Flügel entsprechend weniger oder mehr Auftrieb liefern muß. Bei geringer Fluggeschwindigkeit verändert das deutlich den induzierten Widerstand. Übrigens stellt sich hier heraus, daß ein tragendes Höhenleitwerk die Thermikleistung eines Modells verbessert!

In der Rechnung wurde versucht, den Quertrieb des Höhenleitwerks mit dem Abwindwinkel genauer zu berechnen. Die Ergebnisse erschienen aber sehr unzuverlässig. Deshalb wurden sie durch eine Schätzung ersetzt, welche von der Rechnung in 'Plane Geometry' gestützt wird, letztlich aber willkürlich ist. Dann kann man die Willkür auch zweckdienlich einsetzen: Im Diagramm oben soll natürlich die Kurve des Leistungsbedarfs die Kurve des Leistungsangebotes bei Teillast gerade eben berühren. Ursprünglich lag sie aber um einige Prozent zu hoch und wurde so 'heruntergemogelt', daß es paßt. Dazu wurde eben der Quertrieb des Höhenleitwerks benutzt, aber auch die ebenso willkürlichen Werte Rumpf-Widerstandsbeiwert und Interferenzwiderstand. Die Fluggeschwindigkeit beim Schweben wird dadurch nicht merklich verändert, aber das Diagramm wird merklich schöner.

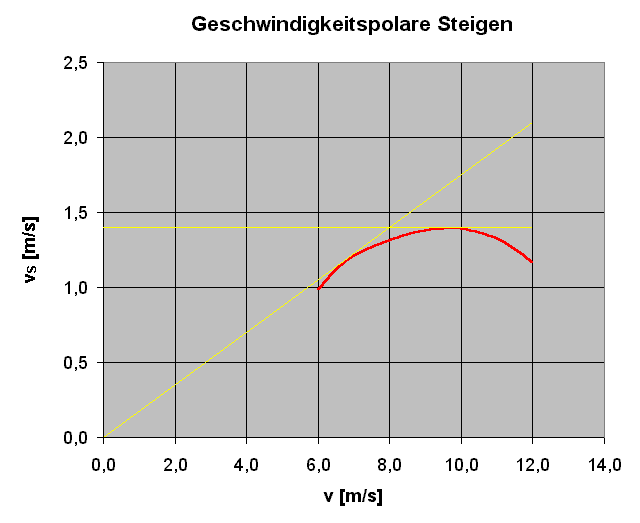
Natürlich beeinflußt der Widerstand die Vertikalgeschwindigkeit, also auch die Steigpolare. Sie zeigt die möglichen Flugzustände bei Vollast des Motors ('Vollgas'). Die 'Mogelei' bleibt aber im einstelligen Prozentbereich, wo wir auch die Genauigkeit bzw. Unsicherheit der Rechnung vermuten. Bei der Steigpolare spielt der Antrieb des Modells eine ebenso große Rolle wie die Zelle. Dessen Berechnung stützt sich aber auf - wenn auch nur wenige - Messungen und sollte ebenso genau oder ungenau sein. Die beiden Tangenten zeigen anschaulich die Fälle 'steilstes Steigen' und 'schnellstes Steigen', zu denen man Horizontal- und Vertikalgeschwindigkeit aus dem Diagramm entnehmen kann. Negative und positive Auswirkungen des Propellerstrahls, wie z.B. höherer Auftrieb, wurden vernachlässigt.

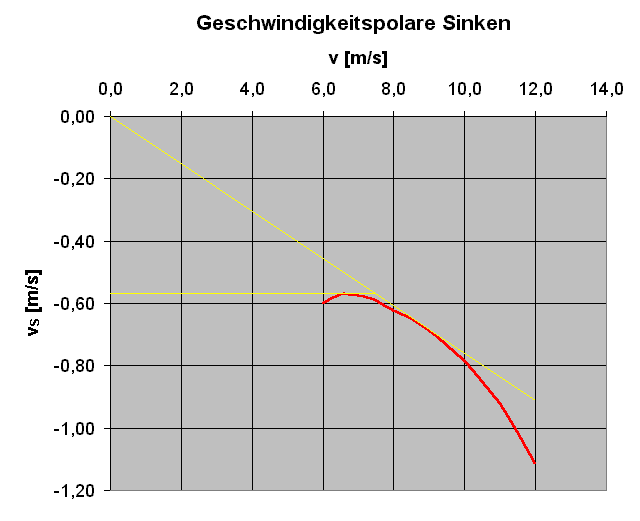
Die Sinkpolare zeigt die möglichen Flugzustände bei abgeschaltetem Motor. Ein Widerstand des Propellers wurde vernachlässigt. Bei stehendem Propeller sollte der recht klein sein, weil der Prop klein ist und der Rumpf relativ viel größeren Widerstand hat. Ein mitlaufender Propeller (windmilling) wird ausgeschlossen. Die beiden Tangenten zeigen anschaulich die Fälle 'geringstes Sinken' und 'flachstes Sinken', zu denen man Horizontal- und Vertikalgeschwindigkeit aus dem Diagramm entnehmen kann.

Zusammenfassung

Bei aller gebotenen Vorsicht: Die Polaren geben die Flugleistungen des Brummi zumindest annähernd korrekt wieder. Das heißt, daß die Steig-, Sink- und Horizontalgeschwindigkeiten, vor allem die Größenordnung und das Verhältnis zueinander, einigermaßen stimmen. Die folgende Tabelle faßt die wichtigen Flugzustände zusammen, geordnet nach Vertikalgeschwindigkeit. P_Zelle ist der Leistungsbedarf des Modells aus dem Widerstand, P_Steigen die für Steigen aufgebrachte 'Hubleistung'. P_mech ist die an den Propeller abgegebene mechanische Leistung, P_el die vom Akku abgegebene elektrische Leistung. Der Gesamtwirkungsgrad gibt an, wie viel von der Akkuleistung 'beim Modell ankommt', und sollte, wie die anderen Zahlen, nicht absolut, sondern zum Vergleich der Flugzustände genommen werden.

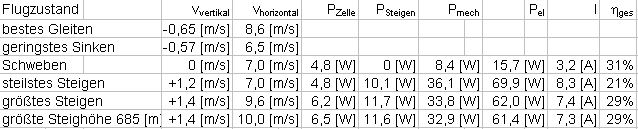
Gewohnt ist, daß Schweben mit minimaler Leistung und geringstes Sinken, aber auch steilstes Steigen bei sehr geringer Horizontalgeschwindigkeit liegen. Auffallen könnte schon eher, daß die angenommene 'normale' Geschwindigkeit im Horizontalflug (8 m/s) kleiner ist als diejenige beim flachsten Sinken oder beim schnellsten Steigen. Auffallen sollte aber, daß der größte Höhengewinn bei einer sehr hohen Geschwindigkeit erreicht wird. Zwischen dem schnellsten Steigen und dem größten Höhengewinn ist zwar kaum ein Unterschied. Auch 'kneifen' (zu steil steigen) verringert die Steiggeschwindigkeit nur wenig (wohl den Höhengewinn, siehe Wirkungsgrad). Aber es kann schon paradox wirken, wenn man das Modell zum Steigen besonders schnell machen soll, zumal der Steigwinkel dann flach ist und nicht der Eindruck schnellen Steigens entsteht.

Das Modell an sich (die Zelle) würde bei geringer Geschwindigkeit am besten steigen. Der Antrieb unter Vollast hat aber - wegen der großen Steigung des Propellers - seinen besten Wirkungsgrad bei hoher Geschwindigkeit. Effektiv liegt die Geschwindigkeit des besten oder höchsten Steigens dazwischen. Nach den Empfehlungen von MULTIPLEX für den Motor darf man allerdings keine Art von Steigflug längere Zeit durchführen, weil die Ströme zu hoch sind. Maximal 8 A für eine Minute gilt praktisch immer, geringerer Strom bedeutet geringeren Wirkungsgrad. Aber in einer Minute steigt der Brummi 80 m und ist dann schon schlecht zu erkennen. Es sollte also praktisch kein Problem geben, besonders wenn Kühlluft zugeführt wird.

Die hier aufgeführten berechneten Werte sind mit Sicherheit ungenau, aber das Verhältnis, die Reihenfolge zueinander stimmt. Das läßt sich durch den Eindruck sagen, den man vom Flug des 'richtigen' Modells hat. Auch das simulierte Modell zeigt das gleiche Verhalten, und der Simulator zeigt sogar die erwarteten Geschwindigkeiten an. Das ist allerdings kein vollständiger Beweis, weil berechnete Werte (Antriebskennlinie, Profilpolare) in das Simulatormodell eingehen und es sich insofern nur selbst bestätigt. Die Vertikalgeschwindigkeiten konnten aber mit dem Picolario auch am 'richtigen' Modell nachgewiesen werden. Hier wäre eine komplette Telemetrie interessant, die sehr leicht sein müßte.

Links and Downloads

Meine Berechnungen des Brummi-Antriebs und der Flugleistungen sind als Excel-Datei mit mehreren Rechenblättern verfügbar, einschließlich aller Formeln. Falls jemand darin Fehler entdecken sollte, wäre ich für eine Nachricht durchaus dankbar.

Wer den REFLEX-Modellflugsimulator besitzt, kann die quantitative Betrachtung des Brummi auch darin nachvollziehen. Hier gibt es den Brummi als REFLEX-Modell, und auf einer eigenen Seite wird es - auch mit Flugeigenschaften - beschrieben.